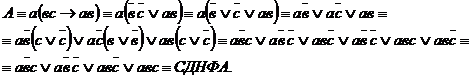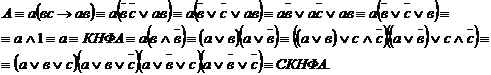Конънктивная нормальная форма и совершенная конъюнктивная нормальная форма

5.3 Конъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма (КНФ и СКНФ)

Определение 4. Элементарной дизъюнкцией n переменных называется дизъюнкция переменных или их отрицаний.

Определение 5. Конъюнктивной нормальной формой (КНФ) формулы А называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Определение 6. Совершенной конъюнктивной нормальной формулы А (СКНФ А) называется КНФ А, удовлетворяющая следующим условиям:

1. все элементарные дизъюнкции, входящие в КНФ А, содержат все переменные;

2. все элементарные дизъюнкции, входящие в КНФ А, различны;

3. каждая элементарная дизъюнкция, входящая в КНФ А, содержит переменную один раз;

4. ни одна элементарная дизъюнкция, входящая в КНФ А, не содержит переменную и ее отрицание.

СКНФ А можно получить двумя способами:

а) с помощью таблицы истинности (используя закон двойственности ) (см. 5.1);

б) с помощью равносильных преобразований.

Правило получения СКНФ из формулы А с помощью равносильных преобразований.

1. Для формулы А получаем любую КНФ А.

2. Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ А.

1) Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную , тогда заменяем В на .

2) Если в некоторую элементарную дизъюнкцию В переменная входит дважды, то лишнюю переменную нужно отбросить, так как .

3) Если КНФ А содержит две одинаковых элементарных дизъюнкций, то одну можно отбросить, так как .

4) Если в элементарную дизъюнкцию входит пара , то ее можно отбросить так как , а истинное высказывание из конъюнкции можно выбросить (в силу равносильности ).